发布于 

Datalog - declarative logic programming language

翻译自 Introduction to Datalog

Introduction to Datalog

Logic programming

与命令式编程范式不同，声明式编程 表达了计算的逻辑，而不显式指定其控制流。也就是说，声明式编程关注的是“做什么”（what），而不是“如何做”（how）。如果你以前曾研究过声明式编程，你可能已经读到过类似的描述。如果这是你第一次接触声明式编程的相关内容，那么在开发一个应用时不专注于如何实现，可能会让你感觉非常陌生——对于我来说，最初也是如此！

然而，很可能你已经在不知不觉中使用过声明式编程！实际上，像 HTML、CSS 和 SQL 这样的广泛使用的领域特定语言都属于 声明式编程范式。例如，HTML 只是描述了网页上应该出现什么，而不关心各种元素应该按什么顺序由浏览器渲染。同样，SQL 查询只是描述了要返回什么，而不关心如何计算返回值。从本质上来说，这就是人们所说的声明式编程关注“做什么”的含义。

值得强调的是，声明式编程实际上是一个广义的术语，除了上面提到的领域特定语言外，它还包含了子范式——逻辑编程。正是这一子范式将在本教程中占据我们的关注重点。

逻辑编程是基于形式逻辑的。这意味着，任何用逻辑编程语言编写的程序（例如 Datalog 或 Prolog）不过是以逻辑形式表达的一组句子，描述了关于某个特定领域的事实和规则。这使得逻辑编程拥有一些其他范式所没有的优点，具体包括：

  • 没有副作用
  • 没有显式的控制流
  • 强有力的终止性保证

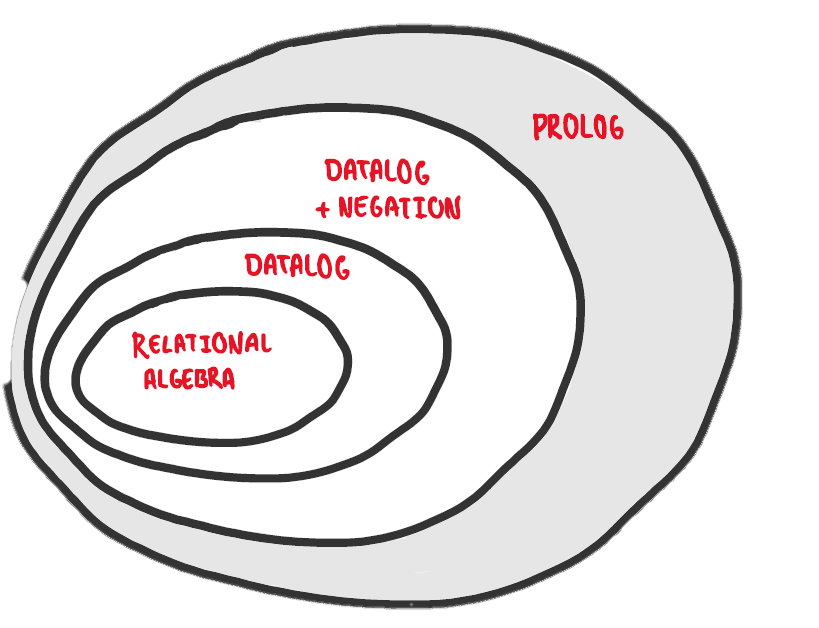
然而，逻辑编程依赖于逻辑形式的句子，这也影响了它的表达能力——即，哪些算法可以通过哪些逻辑编程语言来表达。表达能力的范围是逐层递增的：

  • 关系代数 (Relational Algebra)
    • 最小的表达能力范围，仅限于基本的数据库查询操作（如选择、投影、连接等）。这是关系数据库的理论基础
    • 示例：SQL 中的基本查询功能
  • Datalog
    • 在关系代数的基础上增加了递归的能力，使得可以表达更复杂的查询和规则
    • 示例：用规则定义家谱关系（如“祖父”的定义依赖于“父亲”的关系递归）
  • Datalog + Negation
    • 在 Datalog 的基础上进一步扩展，加入了对否定（negation）的支持，使得可以处理带有“不存在”或“不是”的逻辑表达
    • 示例：查询所有不是学生的人
  • Prolog
    • 表达能力最强，支持完全的一阶逻辑。相比 Datalog，Prolog 可以使用函数、动态规则，以及更复杂的推理模式
    • 示例：通过规则和事实模拟复杂的人工智能推理任务

最内层的圆圈包含了关系代数（Relational Algebra），如果你有 SQL 的使用经验，那么对其可能会感到熟悉。Datalog 被展示为对关系代数的直接扩展。我们之所以称 Datalog 是关系代数的直接扩展，是因为 Datalog 支持递归（这是关系代数所不具备的能力），但除此之外功能并不多。如果你对关系代数不熟悉，也无需担心；本教程不会涉及关系代数的实际编写。这里主要关注的是表达能力，以及如何将这些概念置于一个更广泛的视角中。

下一个圆圈 将 Datalog 扩展到了支持否定（negation）的层次。这一扩展允许我们使用所谓的分层 Datalog（Stratified Datalog）来实现任何多项式时间复杂度的算法。值得注意的是，缺乏否定功能的 Datalog（和关系代数类似）在实际应用中几乎毫无用处。因此，除非特别说明，本教程提到的 Datalog 都默认指支持否定的版本。实际上，如果在扩展 Datalog 的同时对否定运算采取一些适当的预防措施，我们仍然能够保持对终止性（termination）的强有力保证。

然而，如果我们希望表达那些超出多项式时间复杂度的算法，就必须进一步扩展 Datalog。这时，我们进入了最外层的圆圈，从而有效地 将 Datalog 转变为 Prolog。Prolog 是一种图灵完备（Turing-complete）的逻辑编程语言，使我们能够表达任何想要的算法。然而，这种新增的表达能力也带来了直接后果——我们失去了对终止性的严格保证。在本教程的最后，我会简要回到 Prolog 相关的内容。

A new way of thinking

通过前面的讨论，我们可以理解，Datalog 本质上是一种非常简单的语言。这也许不足为奇。学习 Datalog 的挑战并不在于掌握复杂的语法、与编译器“斗智斗勇”，或者处理各种繁琐的库。真正的挑战在于，像学习任何一种新的编程范式一样，你需要重新调整自己的思维方式去理解它的概念。这是一种全新的思维方式！

我们已经知道，使用逻辑编程语言（如 Datalog）编写的任何程序，其实是一个 逻辑约束的集合——即以逻辑形式表达的句子。编译器会使用这些约束集合来计算解决方案。请仔细回想一下这一点。是的，确实如此！实际上，当需要求解时，编译器可以自由选择实现解决方案所需的算法和数据结构。我们无法保证编译器总是采用相同的方法，它甚至可能决定并行执行任务！然而，给定相同的输入，编译器总会生成相同的输出。

幸运的是，由于编译器会在幕后处理所有这些“如何做”的问题（how），我们只需要关注写出正确的约束（做什么，what）。这种特性不仅减少了程序员的工作量，还让我们专注于程序逻辑本身，而不是实现的细节。

Facts and rules

所有逻辑程序（也就是逻辑约束的集合）都由有限组的事实和规则组成，Datalog 程序也不例外。这两个概念可以粗略地类比为其他编程语言中的类和函数。简而言之：

  • 事实：对我们所操作的世界的断言
  • 规则：允许从已有事实推导新事实的句子

现在我们了解了事实和规则的基础，那么如何实际编写一个 Datalog 程序呢？很简单！我们从定义一些 事实 开始。比如，假设我们想要用 Datalog 来表示一个按照主要类型分类的电影收藏架，可以这样写：

1
2
3
Movie("Pulp Fiction", "Crime").
Movie("The Hateful Eight", "Crime"). 
Movie("Reservoir Dogs", "Thriller").

以上代码表示了三个事实，每个事实包含两个值（用逗号分隔），并以 .（句号）结束。在这个例子中，第一个值是电影标题，第二个值是电影类型。每个事实的谓词名称为 Movie。

如果我们想要进一步扩展我们的“世界”，比如添加每部电影的演员，可以这样：

1
2
3
StarringIn("Pulp Fiction", "Tim Roth").
StarringIn("The Hateful Eight", "Tim Roth").
StarringIn("Reservoir Dogs", "Harvey Keitel").

同样的逻辑可以应用于电影的导演：

1
2
3
DirectedBy("Pulp Fiction", "Quentin Tarantino").
DirectedBy("The Hateful Eight", "Quentin Tarantino").
DirectedBy("Reservoir Dogs", "Quentin Tarantino").

通常，将所有事实写在程序的开头是一个好习惯，以便程序结构更清晰。如果你更喜欢按照字母顺序组织，Datalog 也支持这种灵活性。在定义事实时，参数的顺序并不重要，例如：

1
2
DirectedBy("Reservoir Dogs", "Quentin Tarantino").
DirectedBy("Quentin Tarantino", "Reservoir Dogs").

两者都是有效的。但是，写规则时必须遵守你选择的顺序（稍后会详细解释）。

现在，我们已经使用事实建模了我们的电影收藏。假设有一位朋友特别喜欢犯罪类型的电影，并且尤其偏爱由 Quentin Tarantino 执导且由 Tim Roth 主演的电影。如何根据这些偏好挑选出合适的电影？

显然，可以通过手动阅读上述事实找到答案。但如果我们的电影集合包含数以万计的标题（比如 Netflix 的规模），这种手动方法将变得不可行。这时候，规则就派上用场了！

我们可以定义一条规则来解决这个问题：

1
2
3
4
ExtraAwesomeMovie(title) :-
    Movie(title, "Crime"),
    StarringIn(title, "Tim Roth"),
    DirectedBy(title, "Quentin Tarantino").

这条规则的含义是：

  • 如果有一部电影 title 的类型是 “Crime”（犯罪类型）
  • 且这部电影由 Tim Roth 主演
  • 并且由 Quentin Tarantino 执导
  • 那么我们可以推导出这部电影是 ExtraAwesomeMovie

规则中的 :- 读作“如果”（if），表示 物质条件，左侧是 结果，右侧是 条件。当 Datalog 程序运行时，规则会匹配程序中所有可用的事实，仅返回满足该规则的事实。在这个例子中，只有符合规则条件的电影会被推导为 ExtraAwesomeMovie。

匹配规则时的注意事项

  • 额外的事实不会干扰规则匹配

    • 比如，如果程序中有额外的事实：FirstName("Jennifer").
    • 虽然这个事实会被规则扫描，但它不会满足 Movie 的谓词，也不会干扰规则的正常运行。

  • 事实中参数顺序的重要性

    • 在事实定义中，参数顺序无关紧要，但在规则中必须遵守定义的顺序。

    • 例如：Movie(title, "Crime") 和 Movie("Crime", title) 是不同的，第一种匹配犯罪类型的电影并返回标题，第二种只匹配标题为 “Crime” 的电影并返回类型。

根据 ExtraAwesomeMovie 规则，从我们的事实集合中推导的结果是：

1
2
ExtraAwesomeMovie("Pulp Fiction").
ExtraAwesomeMovie("The Hateful Eight").

这表明，这两部电影都满足朋友的偏好，可以被归类为 ExtraAwesomeMovie。我们可以基于这些推导出的结果放心推荐给朋友。

Datalog Syntax

在 Datalog 中，事实和规则都用 Horn 子句（Horn Clauses） 来表示。虽然本篇文章不会深入介绍 Horn 子句的具体细节，但如果你感兴趣，可以查阅相关的进一步资料。这里我们只需要了解以下几点：

  • Horn 子句是一种逻辑子句，它最多包含一个正文字面量（positive literal）
  • 根据 Horn 子句的用途，可以将其分为三种类型：
    1. 事实（Facts 或 Unit Clauses）：用于表达无条件的知识
    2. 规则（Rules）：用于表达有条件的知识
    3. 目标子句（Goal Clauses）：用于表示目标（后续将详细介绍）

我们已经介绍了前两种类型（事实和规则），稍后会回到第三种类型（目标子句）。Datalog 的完整语法如下：

$$
P∈Program = c_1,…, c_n\
c∈Constraint = a_0⇐a_1,…, a_n\
a∈Atom = p(t_1,…, t_n)\
t∈Term = k ∣ x\
$$

其中：

  • $p$：有限集合的 谓词符号
  • $k$：有限集合的 变量符号
  • $x$：有限集合的 常量

换句话说，一个 Datalog 程序 $P$ 由一系列约束 $c_1,…,c_n$ 组成。这种设计意味着最短的 Datalog 程序是一个空的约束序列。约束 $c$ 是一个 Horn 子句，由一个头部原子 $a_0$ 和一个可选的主体原子序列 $a_1,…,a_n$ 组成。如果主体为空，则这是一个事实；否则，这是一个规则。原子 $a$ 由一个谓词符号（即一个名称）和一系列项 $t_1,…,t_n$ 组成。项 $t$ 可以是一个常量（例如字符串 "Crime" 或整数 31），或者一个变量（例如 title）。以下是可视化的描述：

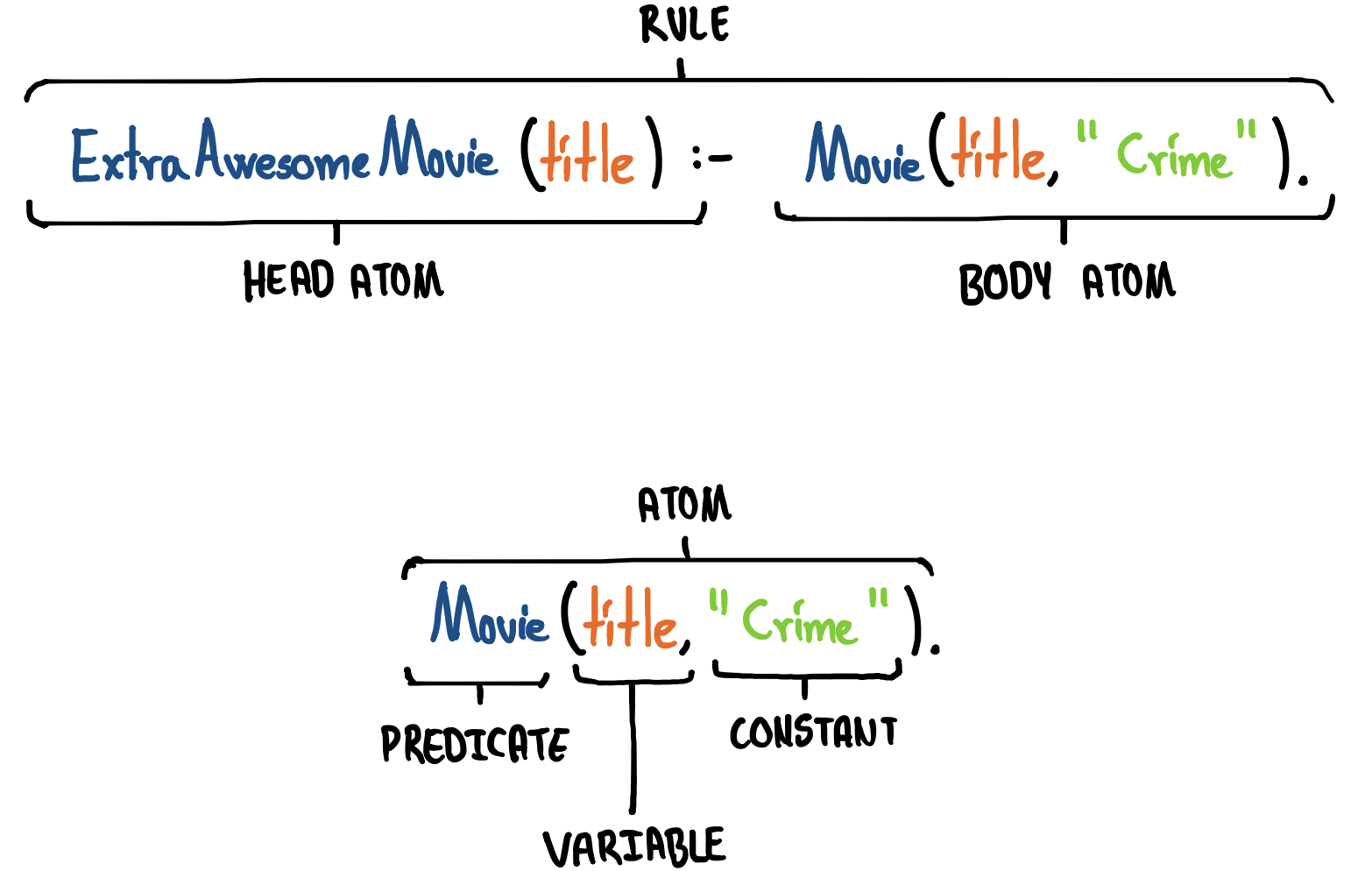
此外，如前所述，行末的 .（句号） 用于结束某个具体的事实或规则。然而，如果我们编写的规则包含多行，那么需要用 ,（逗号） 分隔每一行，最后一行除外，正如上面示例中所示。

不同来源可能使用不同的术语。例如约束（即事实或规则）有时也被称为子句（clause）或简单地称为规则（rule），原子（atom） 有时也被称为文字（literal）。某些论文会明确说明它们采用的术语，如果语境不够清楚的话。

以上内容就是 Datalog 的全部语法。

Groundness and Safety

在 Datalog 中，当一个原子的所有项都是 常量 时，这个原子被称为 grounded。如果包含变量，它就不是 grounded。例如：

1
2
NonGroundedFact("Walter White", actor). 
GroundedFact("Walter White", "Bryan Cranston").

由于 actor 是变量，所以这个事实不是 grounded；因为两项 "Walter White" 和 "Bryan Cranston" 都是常量，所以它是 grounded。

类似地，规则的范围性可以这样理解：

1
2
3
4
5
6
7
NonGroundedRule("Walter White", actor) :-
    MainCharacter("Walter White", "Breaking Bad"),
    StarringIn("Breaking Bad", actor).
    
GroundedRule("Walter White", "Bryan Cranston") :-
    MainCharacter("Walter White", "Breaking Bad"),
    StarringIn("Breaking Bad", "Bryan Cranston").

由于规则中的 actor 变量出现在头部和规则体中，所以这个规则不是 grounded；所有项均为常量，因此它是 grounded。

为了确保我们能够产生有意义的结果，我们引入了 安全性（safety） 的概念。我们认为一个给定的程序 $P$ 是安全的，当且仅当：

  1. $P$ 的每个事实都是 范围化（grounded） 的
  2. 每个出现在规则头部的变量 $x$ 也必须至少出现在规则体中（例如，上述 NonGroundRule 中的 actor 变量同时出现在头部和规则体中），这被称为 范围限制属性（range restriction property）

需要特别强调的是，我们的 Datalog 程序不需要规则本身是完全范围化的（grounded）来保证其安全性；我们只需确保规则头部中出现的变量在规则体中 至少出现过一次 即可。

这些条件确保了从我们的 Datalog 程序中可以推导出的事实集合是 有限的，从而进一步保证了程序的 终止性。大多数情况下，这些条件可能并不是我们在编程时需要主动考虑的问题，因为绝大多数 Datalog 实现会直接拒绝不安全的程序。但现在你知道为什么程序可能会被拒绝了！

Databases

我们将程序中的事实视为我们的数据库。我们利用这个数据库来回答查询——既可以直接读取数据库中已有的信息，也可以像前面通过 ExtraAwesomeMovie 示例所展示的那样，利用已有知识推导出新的知识。在 Datalog 的语境中，查询实际上就是在询问某个条件是否成立（无论通过哪种方式）。我们稍后会更详细地讨论查询。在 Datalog 中，我们具体操作两种不同类型的数据库：

  1. 外延数据库（Extensional Database, EDB）：指的是 Datalog 程序 PPP 中已经存在的事实集合
  2. 内涵数据库（Intensional Database, IDB）：指的是可以从程序 PPP 推导出的事实集合

换句话说，我们可以将 EDB 视为 Datalog 程序的 输入，而将 IDB 视为 Datalog 程序的 输出。

以下是一个简单的 Datalog 程序：

1
2
3
4
5
6
7
8
9
Edge("a", "b").
Edge("b", "c").

Path(x, y) :-
    Edge(x, y).

Path(x, z) :-
    Path(x, y),
    Edge(y, z).

Path 规则表明如果从 $x→y$ 存在路径，且从 $y→z$ 存在边，那么从 $x→z$ 也存在路径

在当前程序中，外延数据库 包含以下两条事实（直接写入程序的）：

1
2
Edge("a", "b").     extensional
Edge("b", "c").     extensional

运行该程序后，根据规则可以推导出以下新事实（推导出来的）：

1
2
3
Path("a", "b").     intensional
Path("b", "c").     intensional
Path("a", "c").     intensional

此时，完整的数据库（即 EDB + IDB 的联合）包含：

1
2
3
4
5
6
Edge("a", "b").     extensional
Edge("b", "c").     extensional

Path("a", "b").     intensional
Path("b", "c").     intensional
Path("a", "c").     intensional

请注意，规则的输出（在此例中为 Path）由新的 范围化原子（ground atoms） 组成——这些原子是具体的事实，具有相同的名称（如 Path），但它们的参数满足规则的条件。以上内容也清楚地表明了为什么我们可以将 EDB 视为程序的输入，将 IDB 视为程序的输出。从语义上讲，Datalog 程序本质上就是 EDB 和 IDB 的联合。

我所称的“数据库”（database）有时也被称为“模式”（schema）。一些论文会分别提到“外延模式（extensional schema）”和“内涵模式（intensional schema）”，不过缩写 EDB 和 IDB 通常保持不变。

Datalog Semantics

在前面的介绍中，我提到了编译器在计算解决方案时发生的“魔法”。事实上，我们对编译器的操作方式并非完全一无所知。实际上，Datalog 有三种不同但等价的语义：

  1. 模型论语义（Model-theoretic semantics）
  2. 固定点语义（Fixed-point semantics）
  3. 证明论语义（Proof-theoretic semantics）

这三种语义共同构成理解 Datalog 程序的关键。通过研究这三种语义，我们可以获得足够的理解和知识，从而合理地推导 Datalog 程序的解决方案。

Model-theoretic semantics

Fixed-point semantics

Proof-theoretic semantics

Datalog with Negation

Problems with negation

Stratified negation

Precedence graphs

Prolog

快来参与讨论吧