攻击树/图技术总结 😈⃤
感知和理解网络攻击是一项困难的任务,需要借助有效的技术手段来加以辅助

攻击建模技术
攻击建模技术(AMT)用于建模和可视化一系列事件和/或事件组合,这些事件使得对计算机或网络的网络攻击能够成功实施。

AMT 大致可以分为三类:基于用例框架的方法、基于时间维度呈现的方法、基于图形的建模方法
AMT 不仅能够帮助观察者分析网络攻击场景,还减轻了安全专家在评估攻击和制定缓解措施时的认知负担。通过简化复杂信息的表达,它使决策者更快掌握安全问题,更好地感知风险,并直观理解复杂概念。AMT 提供了高效的工具和工作空间,促进了更清晰的讨论和辩论,同时在较少依赖逻辑模型的情况下支持对网络攻击的感知和理解。
攻击建模中的术语分类
- 前提条件(Precondition)用于描述网络攻击成功所需的先决条件
- 相关术语包括:Exploit、Prerequisite、Precondition、Predicate、Requires 等
- 后置条件(Postcondition)描述网络攻击完成后产生的后果或效果
- 相关术语包括:Postcondition、Effect、Provides、Consequence、Impact 等
- 实施者(Perpetrator)表示进行网络攻击的主体
- 相关术语包括:Perpetrator、Attacker、Adversary、Hacker、Misuser、Bad guy 等
攻击模型的可视化
攻击模型通常通过组合二维形状(如正方形、矩形和椭圆)、一维形状(如线条)以及文本语法来构建,用以表示网络攻击的结构。这种表达方式被称为视觉语法、视觉修辞或视觉符号体系。
故障树和 Petri 网等建模系统的视觉语法已经实现标准化,它们在模拟网络攻击时能够形成一致的理解框架。然而,攻击图和攻击树在视觉语法上缺乏标准化、规范化方法以及通用的建模框架。许多研究者使用自创且未经验证的视觉语法来模拟攻击,这种方法被亚历山大称为“无意识设计方法”。
目前,有超过 75 种攻击图可视化语法配置和超过 20 种攻击树配置,这些配置涵盖了 180 多种不同的可视化语法。这些可视化语法在用于表示网络攻击中关键构造(如先决条件和漏洞)的形状和形式上存在显著差异。如此多的相互冲突的提案不仅容易让研究人员和从业者在选择时感到困惑,也反映出该领域的“不成熟”,并导致研究工作的“分散化”。
网络攻击
网络攻击相关术语
| 术语 | 解释 |
|---|---|
| 漏洞 (Vulnerability) | 一种可被利用的、意外存在的系统弱点,由一个或多个前提条件的存在而导致 |
| 前提条件 (Precondition) | 系统中为了成功利用漏洞而必须满足的状态 |
| 初始前提条件 (Initial precondition) | 网络攻击中需要满足的第一个前提条件 |
| 攻击者能力 (Perpetrator capability) | 攻击者运行漏洞利用所需的工具、知识和/或访问权限级别 |
| 后置条件 (Postcondition) | 成功利用漏洞后产生的条件或状态 |
| 目标 (Goal) | 网络攻击的最终目标 |
| 利用 (Exploit) | 一系列步骤 —— 包括执行代码或手动操作,利用目标系统中的一个或多个漏洞,并为攻击者提供特定的能力 |
| 非侵入性事件 (Non-intrusive event) | 支持和辅助网络攻击的事件,但不会改变目标系统的状态 |
脆弱性、前提条件和后置条件
- 脆弱性
- 脆弱性是指系统设计、实施或管理中存在的可被利用的弱点
- 脆弱性通常由多个系统状态的组合构成,这些状态被称为前提条件
- 前提条件
- 前提条件是指一组系统属性,漏洞的利用必须具备这些属性才能成功执行
- 初始前提条件是系统固有的属性,并非由于漏洞利用而产生
- 通过解决这些前提条件,可能会使攻击中的所有后续步骤失效,至少有 三种类型的前提条件:
- 状态/服务:目标系统持有或宣称特定版本的操作系统、系统软件/应用程序、服务,或处于特定的硬件/软件状态
- 可达性:目标是可访问的
- 攻击者能力:攻击者具备某些特定能力,例如能够在目标系统上运行进程、使用工具、拥有特权级别,或具备攻击工具和必要的技能
- 在上述前提条件类型中,状态/服务 通常在 AMTs 中表示,如攻击图和攻击树,可达性和攻击者能力的表示则较为少见
- 实施者能力是攻击分析中的关键因素之一,对于 安全分析师 而言,了解哪些漏洞需要较高的实施者能力,哪些漏洞对实施者的能力要求较低,至关重要。例如,在 RPC(远程过程调用) 漏洞中,实施者能力的要求如下:
- rcp 服务必须对攻击者可用
- 目标主机必须信任源主机
- 攻击者必须具备本地 shell 访问权限
- 后置条件
- 成功的漏洞利用会导致一个或多个后置条件,虽然漏洞利用的结果通常被称为后置条件,但这些后置条件有时也可以成为进一步漏洞利用的前提条件
- 因此,大多数研究人员将后置条件视为前提条件的延伸,并且 使用“目标”一词来指代最终的后置条件
条件逻辑
要成功利用漏洞,必须满足一个或多个前提条件,这些前提条件的组合可以通过前提条件逻辑来表示。例如,
- 给定两个前提条件:pr1 和 pr2
- 如果需要同时满足这两个条件,则可以用如下形式的 合取表示:pr1 ∧ pr2
- 如果只需满足其中任意一个条件,则可以用如下形式的 析取表示:pr1 ∨ pr2
尽管前提条件逻辑的表示对于识别网络攻击的防御和应对措施至关重要,但许多攻击图很少涉及前提条件逻辑的具体表示。
漏洞利用
漏洞利用是一组通过代码或手动步骤执行的操作,旨在利用目标系统中的一个或多个漏洞,为攻击者提供特定功能。
漏洞利用可以被定义为以下形式的表达式: **利用(漏洞,后置条件,来源,目标)/ exploit(vulnerability, postcondition, source, target)**,其中:
- 漏洞:被利用的脆弱性,漏洞可以分解为多个前提条件,所有这些前提条件或它们的组合必须存在,漏洞才能被利用
- 后置条件:漏洞利用产生的结果
- 来源(source):源主机,即发起漏洞利用的主机
- 目标(target):漏洞利用的目标主机
以下是漏洞形式表达的一些示例:
- **ftp_rhosts(ftp, trusthost, i, j)**:表示主机 i 利用主机 j 的 FTP 漏洞,并将受信任主机列表上传到主机 j
- **sshd_bof(sshd, root, i, j)**:表示主机 i 利用主机 j 的 SSH(安全 Shell)服务中的缓冲区溢出漏洞,从而获得对主机 j 的 root 访问权限
- **local_bof(bofv, root, i, j)**:表示主机 i 利用主机 j 中的本地缓冲区溢出漏洞(bofv),从而获得对主机 j 的 root 访问权限
目前文献中并没有关于漏洞利用和漏洞形式化表达的统一标准或协议
非侵入事件
非侵入事件,也称为二次漏洞利用或可疑事件,是攻击者用于发现目标系统属性和漏洞的系统探测操作。与漏洞利用不同,非侵入事件不会改变系统属性,除非目标系统对这些事件作出程序化或手动的反应,例如阻塞端口或创建新的入侵检测系统规则。
非侵入事件的示例包括 rpcinfo,该工具能够显示目标机器上的端口和服务数据,以及各种探测和扫描工具,如 nmap、netcat、amap、XProbe、P0f 和 X-Scan。这些工具会返回系统的响应信息,但不会改变系统的状态。
入侵检测系统(IDS)能够检测并警告侵入事件(漏洞利用)和非侵入事件。
| 签名(漏洞利用) | 前提条件 | 后置条件 |
|---|---|---|
| RPC sadmind UDP PING | 主机数据的泄露 | 运行服务的泄露;系统访问(非侵入) |
| RPC portmap sadmind request UDP | 主机数据的泄露 | 端口号的泄露;运行服务的泄露;系统访问;远程访问(非侵入) |
| RPC sadmind UDP NET-MGT_PROC_SERVICE CLIENT_DOMAIN overflow attempt | 主机数据的泄露;端口号的泄露;运行服务的泄露 | 系统访问;远程访问;管理员访问(侵入) |
| RPC sadmind query with root credentials attempt UDP | 主机数据的泄露;端口号的泄露;运行服务的泄露;系统访问;远程访问 | 远程访问;管理员访问(侵入) |
如表所示,一些事件(如 RPC sadmind UDP PING 和 RPC portmap sadmind request UDP)既可以是侵入事件,也可以是非侵入事件。RPC sadmind UDP PING 会泄露主机的一些信息——这是非侵入事件,而 RPC portmap sadmind request UDP 则会提供对主机的系统访问权限——这是侵入事件,侵入事件和非侵入事件可以统称为 漏洞利用。
网络攻击
网络攻击是一组包含一个或多个漏洞利用的操作,这些操作以顺序或并行的方式应用于目标系统,以暴露目标系统的漏洞并改变其状态。
一旦漏洞被利用,就会产生多个后置条件,这些后置条件中的每一个都可能成为进一步利用的前提条件。攻击的最终目标在攻击树和攻击图中被称为“目标”,而在故障树中则被称为“不良条件”。
值得注意的是,不同的观察者对网络攻击的视角可能有所不同。Moody 将这种视角差异称为“认知契合原则”。分析师通常对网络攻击的 低层次技术视角 感兴趣,特别是攻击所需的前提条件和具体的漏洞。他们有时需要向非技术领域的人员解释网络攻击。而非专家,如利益相关者、高管和决策者,更倾向于从 高层次的视角 看待网络攻击,这种视角通常 隐藏了技术细节。然而,在某些情况下,从分析师的技术视角来看待网络攻击也可能对他们有所帮助。
攻击路径
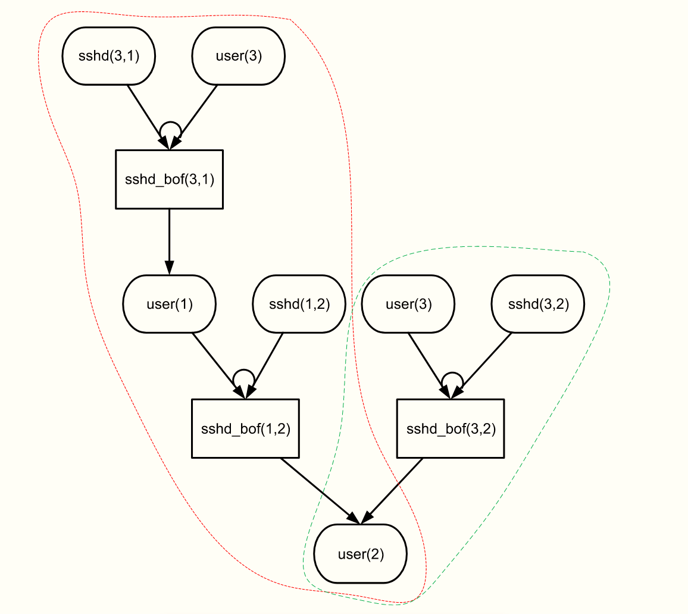
通常情况下,存在多种替代的攻击序列,每一种序列都可能导致攻击成功,这些被称为 攻击路径,并且在所有攻击模型(AMT)中都有表示。上图示例,其中包含两条攻击路径,可以描述为:
- 路径 1:
sshd(3,1) ∧ user(3) → sshd_bof(3,1); user(1) ∧ sshd(1,2) → sshd_bof(1,2) → user(2) - 路径 2:
user(3) ∧ sshd(3,2) → sshd_bof(3,2) → user(2)
攻击路径分析 等技术通过概述已知和预测的攻击事件序列,有助于调查攻击图中的漏洞路径。这种分析能够帮助识别攻击路径中可能受影响的资源,以及路径上的具体漏洞。
上图展示了攻击图和攻击树在视觉表示上的另一个显著差异 —— 事件流方向。图中事件流采用 自上而下 的方式呈现,即观察者从顶部开始阅读,然后按事件顺序向下推进,在调查的 118 个攻击图配置中,有 102 个(86.4%)以自上而下的方式呈现事件;而在调查的 61 个攻击树中,有 59 个(96.7%)采用了自下而上的事件流表示。
上图还说明了攻击图和攻击树在可视化表示方面的另一关键区别,尽管该攻击图仅表示单个攻击目标(user 2),并展示了两条通向该目标的路径,但攻击图经常被用来表示具有多条路径和多个目标的复杂攻击,Aguessy 指出,攻击树的局限性在于它们仅能表示单一攻击,而攻击图则可以表示多个攻击。
结合攻击路径分析和加权边辅助攻击预测的一个示例是 Frigault 和 Wang 提出的 基于贝叶斯的攻击图,在这一示例中,攻击图使分析人员能够计算 成功攻击路径的概率。图中的每个节点代表一个潜在漏洞,以及与该漏洞相关的前提条件和后置条件,每个节点都被分配一个概率,用以表示 该漏洞被利用的可能 性。
Aguessy 提到的攻击图分为 完整攻击图 和 部分攻击图。完整攻击图概述了给定网络中所有潜在漏洞和可能的攻击路径。部分攻击图(也称为 最小攻击图)则概述了给定攻击中节点之间的交互模式。在 Stuxnet 和 Jeep Cherokee 攻击场景,以及分析复杂网络问题时,完整攻击图的表示能力尤为重要。
总体而言,攻击树通常仅表示单一攻击,而 攻击森林(攻击树的集合)是为解决这一局限性而提出的扩展方法。
攻击图应用
攻击图在系统强化中的应用
| 预测策略 | 方法与内容 | |
|---|---|---|
| 事件预测 | 度量事件的可能性 | 使用马尔可夫决策过程计算攻击成功的概率;超警报相关图和攻击策略图;受损置信指数;邻接矩阵聚类;警报相关矩阵;关联规则挖掘;未来场景排序;基于概率的攻击预测;吸收马尔可夫链用于漏洞分析和辅助评估妥协可能性的马尔可夫奖励模型;预测攻击图;pwnPr3d; |
| 分析多步攻击 | 警报聚类、警报合并与意图识别;警报关联框架;因果关联;聚类邻接矩阵;分而治之框架;分层聚类算法;漏洞依赖图; | |
| 攻击路径分析 | 攻击链分析;计算实施攻击的难度;关联规则挖掘; | |
| 多样的 | 加强安全弱点 | 使用利用图;拓扑漏洞分析; |
| 优先移除漏洞 | 技能水平分析;最小关键攻击集(MCSA);预测图;网络强化图;基于博弈论的方法; | |
| IDS 警报相关性分析 | 超警报相关图;ADEPTS;关联规则挖掘算法;拓扑漏洞分析(TVA); | |
| 确定最佳设备配置 | 识别关键设备 | AssetRank 算法; |
| 确定最佳设备部署位置 | 拓扑漏洞分析;成功测量模型; | |
| 最佳设备配置 | 基于图的网络漏洞分析;聚类邻接矩阵;使用 PageRank 排名的攻击图;依赖攻击图;最佳 IDS 部署;NetSPA;攻击响应图; | |
| 预测配置设置的影响 | 反向图遍历识别关键前提条件和漏洞;排序攻击图;邻接矩阵聚类方法和可达性分析;预测图;分层聚类算法; |
攻击树/图
| 特性 | 攻击树 | 攻击图 |
|---|---|---|
| 结构 | 树状结构,简单直观,逻辑清晰 | 图状结构,能表示更复杂的关系和路径 |
| 适用场景 | 单一目标、静态分析、小规模系统 | 多目标、动态分析、复杂系统 |
| 逻辑复杂度 | 支持简单的逻辑(AND/OR 节点) | 支持多路径分析和循环关系,表达更灵活 |
| 分析能力 | 聚焦于一个目标的分解,适合单一攻击目标 | 全面分析所有可能路径,适合多阶段攻击(如 APT)的建模 |
| 易用性 | 易于构建和理解 | 结构复杂,可能需要算法支持 |
| 动态性 | 通常为静态分析工具 | 可支持动态分析,结合实时监控数据更新状态 |
攻击图和攻击树都是基于图形的网络攻击表示,重要的是区分基于图论的图形和树的表示。在图论中,树是一种无环图,其中任意两个顶点之间都有一条路径相连,而图则是一个可能包含环的图。通常决策树、事件树、攻击树、故障树以及 Petri 网的可视化表示符合树的定义,因为它们在可视化时呈现为无环图。
图形的定义
基于图形的网络攻击表示可以用以下形式表示:$G(V; E)$,其中包含 顶点 $v \in V$ 和 边 $e \in E$,边表示节点之间的关系,整体图形结构可以表示为一个元组,形式为 $G = (S, \tau, S_0, S_s, L, EX)$,其中:
- $S$ 是一个有限的状态集
- $\tau \subseteq S \times S$ 是一个转换关系
- $S_0 \subseteq S$ 是初始状态集
- $S_s \subseteq S$ 是成功状态集 —— 例如,获得某一主机的 root 权限或用户权限
- $L : S \to 2^{AP}$ 是状态的标签,标记一组原子命题 (AP)
- $EX$ 是一个有限的漏洞集合,表示两个状态之间的转换
顶点 ($V$) 也称为节点,可以表示:
- 已应用或可能应用于给定节点的漏洞
- 一个前置条件或后置条件
- 前置条件和后置条件的组合
边 ($E$)
- 可以是有向的 —— 表示特定的转换
- 也可以是无向的 —— 表示两个节点之间的通用连接,指示漏洞的执行
通常,攻击树使用顶点表示漏洞,而不表示前置条件,前置条件在从一个漏洞到下一个漏洞的转换中被假定已经满足;攻击图则同时表示前置条件和漏洞。在调查的 118 种 攻击图 配置中,有 98 种(83%)明确表示了 前置条件作为一个节点。然而,在 61 种 攻击树 中,只有 4 种(6.5%)使用不同的形状表示前置条件和漏洞
加权边,可以为边或顶点分配权重,以表示成本、概率、风险或其他度量,这些度量表示:
- 执行某种类型攻击的难度,或者某种攻击成功的概率/可能性
- 成本可以以连续值表示,也可以以布尔值表示
- 布尔值,如:容易和不容易、昂贵和不昂贵、具有侵入性和不具有侵入性等
- 连续值,如:防御/攻击的货币成本、达到/反击的时间、攻击/防御的资源成本等
- 攻击预测 算法通常基于贝叶斯网络或马尔可夫决策过程,这些算法依赖于加权边提供的度量,例如:
- 基于行为的攻击图衡量关键资源被攻破的风险
- 概率攻击图计算网络的年化损失期望值,以帮助优先修补漏洞
- 以及通过三个概率度量(漏洞成功概率、成功发生概率和条件获得概率)来分别衡量成功攻击的可能性、攻击已被应用的可能性和攻击者将达到给定条件的可能性
攻击树
Weiss 于 1991 年引入了 威胁逻辑树,并提供了一个包含风险测量和前提条件逻辑的示例。普遍认为,攻击树 的开创者是 Schneier,其于 1999 年发表的论文被广泛认定为攻击树的奠基之作。攻击树自下而上展示网络攻击,它使用矩形、椭圆等形状,或不使用形状的纯文本来表示前提条件或漏洞。
事件树 和 决策树 的视觉结构与攻击树相似,事件树侧重于系统中的成功与失败,而决策树则侧重于系统故障。尽管事件树和决策树在计算机/网络安全领域中已有应用,但这两种方法尚未得到广泛普及。
故障树与攻击树具有相同的树形结构。故障树的符号表示法最早由美国核管理委员会提出,之后,IEC 于 1990 年、欧洲空间标准化合作组织和英国标准协会对其进行了标准化。故障树被广泛应用于多个行业,如航空航天、放射性废物处理、汽车工业以及计算机系统故障分析。尽管故障树标准是一个通用标准(并非专门针对网络安全领域),但近年来它已成为表示网络攻击的一种流行手段。
故障树是最具视觉表现力的 AMT 之一,因为它们采用了多种标准符号来表达攻击元素,符号集包括多数表决门、优先与(PAND)门、禁止门、非门和顺序门等符号
攻击图
攻击图是一种基于模型的网络安全评估技术。它从攻击者的角度出发,在综合分析多种网络配置和脆弱性信息的基础上,找出所有可能的攻击路径,并提供了一种表示攻击过程场景的可视化方法,从而帮助网络安全管理人员直观地理解目标网络内各个脆弱性之间的关系、脆弱性与网络安全配置之间的关系以及由此产生的潜在威胁。基于攻击图模型的网络安全评估技术是在攻击图的基础上进行深入的安全评估建模和分析,给出安全评估的建议。
攻击图展示了攻击者可能发动的攻击顺序和攻击效果,由顶点和有向边两部分构成。根据攻击图类型的不同,顶点可以表示主机、服务、 漏洞、权限等网络安全相关要素,也可以表示账户被攻击者破解、权限被攻击者获取等网络安全状态,边用于表示攻击者攻击行为的先后顺序。
攻击图起源于 Dacier 的博士论文和两篇早期论文。这些贡献强调了权限图的概念,该图捕获了权限的继承性,在此图中,节点表示用户或一组用户拥有的一组权限,边表示漏洞,状态转换中假定了先决条件。
其他攻击图示的表现形式:
- 漏洞表示为矩形,将先决条件表示为椭圆,先决条件逻辑由圆弧的存在(AND)或不存在(OR)表示
- 漏洞表示为椭圆,先决条件表示为纯文本,未表示出先决条件逻辑
攻击图的核心
规则和推导是攻击图理论的核心,攻击图规则系统与推导引擎的好坏决定了攻击图生成的好坏。
攻击图的生成过程和解决数学推导证明题的过程类似,有:
初始条件(即输入信息)
公理与定理(即攻击图的规则系统)
要证目标(即攻击目标)
所谓攻击路径就是从“初始条件”到“要证目标”的推导过程,将这个推导过程可视化便成了攻击树,由于推导过程可能有多种可能,正如证明一道数学题可能有多种证明方法,就有多条攻击树,形成了攻击图。
攻击图的规则系统就是由许许多多的规则组成,而攻击图的推导引擎依据规则系统自动完成攻击路径的推导。此外,攻击图规则系统决定了该攻击图工具能适用于哪种网络,如使用企业网络的规则系统,则可以适用于企业网络;若使用车联网的规则系统,则可适用于车联网,这也是攻击图理论能适应绝大多数网络形式的原因。
攻击图的类型
| 类别 | 参考文献 |
|---|---|
| “通用”攻击图 | 通用攻击图相关文献 |
| 警报关联图 | 警报关联图;超警报关联图;警报依赖图;入侵图 (i-graph) |
| 漏洞图 | 利用图;面向利用的图;状态枚举攻击图;依赖攻击图;协调攻击图 |
| 杂项攻击图 | 个性化攻击图;主机访问图;混合攻击图;知识图;任务依赖图;贝叶斯攻击图;多先决条件攻击图;证据图;逻辑攻击图;主机受损攻击图;预测攻击图;攻击策略图;特权图 |
| 依赖关系图 | 利用依赖图;混合依赖图;一般依赖图;基于行为的攻击图;概率攻击图;攻击场景图;漏洞原因图;面向利用的图 |
攻击图的作用
在攻击者对网络进行渗透的过程中,特定的连续攻击行为可称为一条由攻击者节点到目标节点的 攻击路径,而攻击图以图形化的方式展示了网络中所有可被防御方发现的攻击路径,对目标网络构建攻击图:
- 一方面可以分析从边界节点到需要进行重点保护节点可能的攻击路径,对路径上的高危节点进行重点防御,达到保护重要节点的目的
- 另一方面可以在攻击发生时实时分析攻击者的攻击能力和推断攻击者的后续攻击目标,以便采取应对和反制措施
在理论上攻击图可以构建完整的网络安全模型,反映网络中各个节点的脆弱性并刻画出攻击者攻陷重要节点的所有途径,弥补了以往技术只能根据漏洞数量和威胁等级评估节点和全网的安全性,而不能根据节点在网络中的位置和功能进行评估的缺陷,因此,攻击图技术很快得到了专家学者的广泛认可,攻击图的代表性科研成果有 TVA ,NetSPA v2,MulVAL 等原型系统
攻击图的核心
攻击图总结
逻辑攻击图
逻辑攻击图主要基于 逻辑推理 来建模漏洞和攻击路径的关系,通常采用 图论 和 逻辑推理引擎 来构建和分析。它的重点是描述漏洞之间的因果关系,帮助分析攻击者可能的行为路径。
主要特征:
- 结构:逻辑攻击图的节点表示网络中的漏洞或攻击目标,边表示从一个漏洞到另一个漏洞的攻击路径。图中的路径表示漏洞被攻击者利用的可能步骤。
- 推理引擎:通常,逻辑攻击图结合了推理技术(如 Datalog、规则引擎)来推导可能的攻击路径。例如,攻击图中的边表示某一漏洞的攻击者可能通过特定漏洞进入系统,或者通过其他漏洞进一步扩展攻击。
- 重点:逻辑攻击图注重通过漏洞和攻击路径的逻辑关系分析攻击者的行动路线。它关注的是如何从一个漏洞逐步到达攻击目标,强调 攻击路径的可行性。
举例: 在一个逻辑攻击图中,某个漏洞(如 SQL 注入)可能是攻击路径的一个节点,而攻击者可能通过这个漏洞进一步攻击数据库系统,从而利用另一个漏洞(如操作系统漏洞)来提升权限。
属性攻击图
属性攻击图是对逻辑攻击图的扩展,它不仅关注 漏洞之间的因果关系,还引入了 漏洞的属性信息。这些属性可以包括漏洞的 严重性、攻击成功的概率、攻击者的可达性 等,这些信息帮助量化网络系统的安全性和风险。
主要特征:
- 属性攻击图的核心特点是每个节点或边都附加了不同的 属性信息,这些属性可能包括:
- 漏洞的 CVSS(通用漏洞评分系统)评分:漏洞的严重性。
- 攻击成功概率:攻击者成功利用漏洞的概率。
- 攻击者技能需求:攻击者需要具备的技能水平。
- 修复状态:漏洞是否已修复或是否已知。
- 计算风险:属性攻击图的目的是在已有攻击路径的基础上,量化每条路径的风险。例如,某条攻击路径可能具有较低的成功概率,但如果路径的漏洞属性严重,仍然可能构成较大的安全威胁。
- 重点:属性攻击图的重点在于 风险量化 和 综合分析。通过引入各种属性信息,攻击图不仅仅显示漏洞间的关系,还提供了关于每条攻击路径的更多细节信息,从而帮助网络安全人员做出更加精准的决策。
举例: 在属性攻击图中,某个漏洞的节点可能会有以下属性:漏洞的 CVSS 分数是 8.5(高风险),并且攻击成功的概率是 70%。另外,这个漏洞的攻击路径可能依赖于其他系统组件的安全性,因此,路径的风险可以通过综合考虑这些属性来评估。
贝叶斯网络
贝叶斯定理 (Bayes’ Theorem)
贝叶斯定理是一个“用新证据更新认知”的数学工具。贝叶斯定理的公式为:
$P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}$,其中:
- $P(A)$:事件 A 发生的先验概率(先验 = 已有的知识)
- $P(B|A)$:在 A 发生的条件下,B 发生的概率(似然概率)
- $P(B)$:事件 B 发生的总概率(全概率)
- $P(A|B)$:在 B 发生的条件下,A 发生的后验概率(后验 = 用新证据更新后的概率)
- 后验概率 = (似然 × 先验) / 全概率
贝叶斯定理的核心思想
- 动态更新认知:先验概率(旧认知) → 加入新证据 → 后验概率(新认知)
- 关注因果关系:区分 $P(B|A)$(已知原因 A,结果 B 的概率)和 $P(A|B)$(已知结果 B,原因 A 的概率)
贝叶斯网络 (Bayesian Network)
- 贝叶斯定理的局限:贝叶斯定理擅长处理两个变量的关系,但现实中问题往往涉及多个变量,且变量间存在复杂的依赖关系
- 贝叶斯网络的诞生:为了简化多变量概率推理,贝叶斯网络用图结构表示变量间的条件依赖关系,将联合概率分解为局部条件概率的乘积
- 贝叶斯网络的核心优势:条件独立性,给定父节点(直接原因),一个节点与其非后代节点条件独立
贝叶斯网络是一个有向无环图(DAG),用节点表示变量,箭头表示因果关系,附带条件概率表(CPT)量化依赖强度,核心组成:
- 节点(Nodes):代表随机变量
- 有向边(Edges):箭头从“因”指向“果”
- 条件概率表(CPT):每个节点存储其父节点给定时的概率分布
构建贝叶斯网络:
- 定义变量及其关系
- 确定变量:选择与问题相关的关键变量
- 绘制依赖关系:通过领域知识或数据分析,画出变量间的因果箭头
- 避免循环:贝叶斯网络必须是有向无环图(DAG)
- 设定条件概率表(CPT)
- 根节点:无父节点的变量,直接设定先验概率
- 中间节点:根据父节点的所有可能组合,填写条件概率
- 若父节点是 $A$ 和 $B$,则 $C$ 的 CPT 需覆盖四种组合(A = 是/否,B = 是/否)
- 概率推断
- 正向推理(预测):已知原因,计算结果的概率
- 逆向推理(诊断):已知结果,反推原因的概率
联合概率 $P(X_1, X_2, \ldots, X_n)$ 表示所有变量 $X_1, X_2, \ldots, X_n$ 同时发生 某个状态的概率
传统计算的难点:如果每个变量有 2 种状态(是/否),3 个变量需要计算 $2^3 = 8$ 种组合的概率;若有 10 个变量,需要计算 $2^{10} = 1024$ 种组合——复杂度指数级增长!
叶斯网络通过图结构揭示变量间的依赖关系,利用条件独立性,将联合概率分解为局部条件概率的乘积:
$P(X_1, X_2, \cdots, X_n) = \prod \limits_{i=1}^n P(X_i | \text{Parents}(X_i))$,每个变量 $X_i$ 的概率仅由其直接原因(父节点)决定,与其他非后代变量无关
贝叶斯攻击图
贝叶斯攻击图(Bayesian Attack Graph)是一种基于贝叶斯网络(Bayesian Network)理论的攻击图,结合了攻击图和概率推理的方法,旨在通过建模漏洞和攻击路径之间的概率关系来量化网络安全风险。这种方法不仅关注攻击路径的因果关系,还考虑了 不确定性 和 攻击成功的概率,提供了比传统攻击图 更为细致和概率化 的安全评估工具。
| 特征 | 逻辑攻击图 | 属性攻击图 | 贝叶斯攻击图 |
|---|---|---|---|
| 建模方式 | 逻辑推理,关注漏洞之间的因果关系 | 逻辑推理 + 漏洞属性(如 CVSS、成功概率等) | 贝叶斯网络,关注条件依赖和概率推理 |
| 处理不确定性 | 无法处理不确定性 | 通过属性信息引入不确定性,支持概率评估 | 强调不确定性的量化,通过概率推理处理不确定性 |
| 风险评估 | 无法量化风险,仅展示攻击路径的可行性 | 能够量化风险,结合漏洞的属性信息评估路径风险 | 通过概率推理全面评估风险,量化各攻击路径的成功概率 |
| 计算复杂度 | 低,适合快速分析和发现攻击路径 | 中等,需考虑属性信息和路径的复杂性 | 高,需要大量的概率计算和推理,适用于复杂网络 |
| 适用场景 | 网络漏洞扫描、路径分析 | 风险量化、漏洞管理、防御策略优化 | 多步骤攻击分析、动态风险评估、大规模复杂网络安全分析 |
Attack Graph Model
- 漏洞的利用被表示为椭圆形的谓词
- 条件则用矩形表示
- 括号中的两个数字分别表示源主机和目标主机
- 攻击者的初始能力通过一个三角形表示
- 目标条件则用一个八边形表示
Bayesian Networks
系统 $X$ 的贝叶斯网络可以形式化地描述为一个对 $B=(G,Q)$,其中 $G$ 是一个有向无环图(DAG),图中的 节点 表示系统的 变量,边 表示变量之间的 条件关系。$Q$ 是一组参数,用于量化网络,如每个变量(节点)的条件分布值。贝叶斯网络的联合概率分布表示为:
$P(X) = \prod_{i=1}^{n} P(X_i | \text{parents}(X_i))$
贝叶斯网络提供了一种紧凑的方式来编码被建模系统中所有的条件关系。
为攻击图(AG)中的每个节点分配一个概率值,表示一个攻击者或攻击者的百分比将利用该漏洞的可能性(为每个节点标注个体概率),然后为攻击图中的每个节点开发条件概率表(CPT),攻击图最终可以表示为一个有向无环图(DAG),并与 CPT 结合,编码所有节点的条件独立性,这将构成一个贝叶斯网络。
将概率分配给节点 比 将概率分配给边 的方法实用,因为节点的概率可以从标准度量中轻松获得,如常见漏洞评分系统(CVSS)
建议使用 CVSS 机制来填充攻击图,这是一种确保使用一致数据的方式(对研究社区对模型产生的结果有信心)
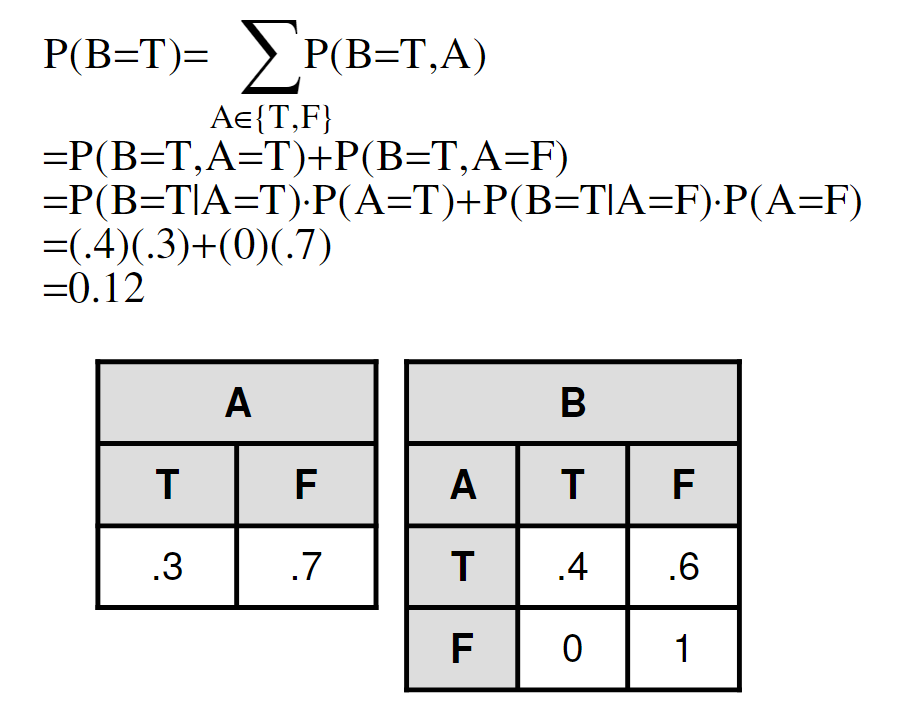
案例 1:要达到目标状态,漏洞 A 和 B 都必须被利用
graph TD;
A((A 0.3)) --> B((B 0.4));
B -->Goal[Goal State];
在这个攻击图(AG)中,每个节点都已注释上一个概率得分,正如之前提到的,模型建议使用 CVSS 提供的评分机制来推导这些概率得分。接下来,为每个节点生成条件概率表(CPT),这些表格编码了每个节点的概率值及其条件依赖关系。在这个模型中,节点被分配了离散值 “T”,表示攻击者成功利用了漏洞,或 “F”,表示攻击者未成功利用漏洞。
条件概率表将帮助计算给定网络的联合概率函数,如前所述,我们的目标是确定达到目标状态的概率,在本案例中,就是计算 $P(B = T)$(即漏洞 B 被成功利用的概率),这个计算可以按以下方式进行:
案例 2:要达到目标状态,必须首先利用漏洞 A 或漏洞 B 中的一个,然后再利用漏洞 C
graph TD;
A((A 0.3)) --> C((C 0.4))
B((B 0.3)) --> C
C --> Goal[Goal State]
案例 2 的概率得分大于案例 1 的得分。这符合直观的性质,即安全度量应该满足这样的概念:当通向目标状态的路径增多时,网络的安全性会降低。因此,这个简单的例子验证了这一概念,并证明了将概率得分作为安全度量的有效性。
案例 3:要达到目标状态,必须首先同时利用漏洞 A 和漏洞 B,然后再利用漏洞 C
graph TD;
subgraph AB ["A and B"]
A((A 0.3))
B((B 0.3))
end
A -->C((C 0.4))
B -->C((C 0.4))
C --> Goal[Goal State]
达到目标状态的概率显著低于案例 1 和案例 2,这在直观上是合理的,因为这个图限制了能够实现利用 C 所需前置条件的潜在攻击者数量。在案例 2 中,能够实现前置条件的攻击者数量是 A“或”B,而在案例 3 中,能够实现前置条件的攻击者数量是 A“和”B。
接下来,将基于案例 2 考虑一个特定情况。在案例 2 中,漏洞 A 和 B 的利用是互相独立的,而在案例 4 中,我们展示了当漏洞 B 的利用概率依赖于漏洞 A 的利用时的影响。这可能是攻击者在成功利用漏洞 A 后,获得的知识使得他更容易利用漏洞 B 的情况。
案例 4:成功利用漏洞 A 增加了利用漏洞 B 的可能性(析取关系)
在案例 4 中,成功利用漏洞 B 的概率,如果没有先利用漏洞 A,评估为 0.3(与案例 2 相同)。然而,假设在成功利用漏洞 A 之后,攻击者获得了知识和技能,增加了利用漏洞 B 的概率至 0.5。
达到目标状态的概率与案例 2 相同。对这一结果的解释是:为了利用 C,我们必须成功利用 A 或 B 中的任意一个。如果 A 被成功利用,那么利用 B 的可能性会增加。然而,攻击者也可以直接攻击 C,而不必尝试利用 B(在这种情况下,调整后的得分没有变化),这与案例 2 相同。如果只有 B 被成功利用,那么 A 不会被利用。这将导致攻击者能够继续攻击 C,且漏洞 B 的得分保持不变。这个情况与案例 2 相同。
案例 5:成功利用漏洞 A 增加了利用漏洞 B 的可能性(合取关系)
这个案例与案例 3 相似,唯一的区别是漏洞 A 和漏洞 B 是相互依赖的,即漏洞 A 的成功利用会增加利用漏洞 B 的可能性。
需要注意的是,结果将始终是漏洞 A 的可能性与调整后的漏洞 B 的可能性得分的合取。这是因为必须先利用漏洞 A,而这意味着,如果漏洞 C 被利用,那么漏洞 B 的可能性将始终等于调整后的值。
案例 6:
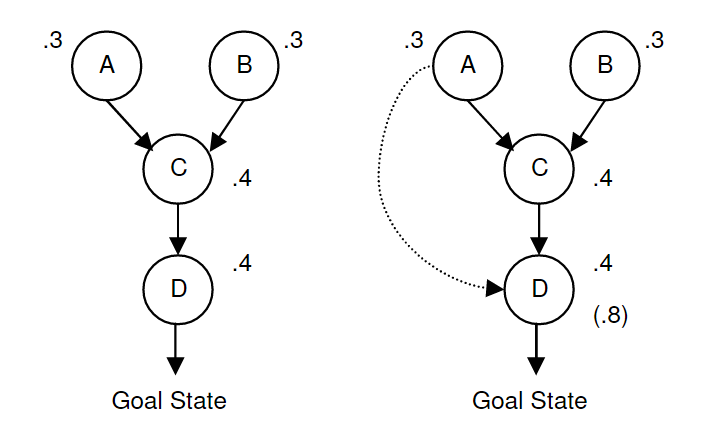
在左侧的图中,攻击者必须:利用漏洞 A 或 B,以及漏洞 C 和 D,才能达到目标状态。右侧的图略有不同。为了达到目标状态,攻击者必须执行与左侧相同的步骤。然而,如果攻击者利用了漏洞 A,他将获得一些知识,这些知识使得利用漏洞 D 变得更容易且更可能。这个关系用可能性得分来表示:当漏洞 A 没有被利用时,漏洞 D 的可能性得分为 0.4;而当漏洞 A 被利用时,漏洞 D 的可能性得分为 0.8。这个关系由下面的条件概率表(CPT)建模。通过贝叶斯网络推理(BN inference),可以计算出达到目标状态的概率得分。这个概率得分表示了所分析网络的整体安全度量。请注意,在右侧图的 CPT 中,利用漏洞 A 意味着利用漏洞 D 的可能性会增加,但漏洞 C 仍然需要被利用。
每个图中达到目标状态的概率得分分别为:左侧为 0.0816,右侧为 0.1296。这个安全度量得分表明,右侧图中达到目标状态的可能性大于左侧图。
参考文献
- Lallie H S, Debattista K, Bal J. A review of attack graph and attack tree visual syntax in cyber security [J]. Computer Science Review, 2020, 35: 100219.
- Wang L, Islam T, Long T, et al. An attack graph-based probabilistic security metric [C]//Data and Applications Security XXII: 22nd Annual IFIP WG 11.3 Working Conference on Data and Applications Security London, UK, July 13-16, 2008 Proceedings 22. Springer Berlin Heidelberg, 2008: 283-296.
- Frigault M, Wang L. Measuring network security using bayesian network-based attack graphs [C]//2008 32nd Annual IEEE International Computer Software and Applications Conference. IEEE, 2008: 698-703.