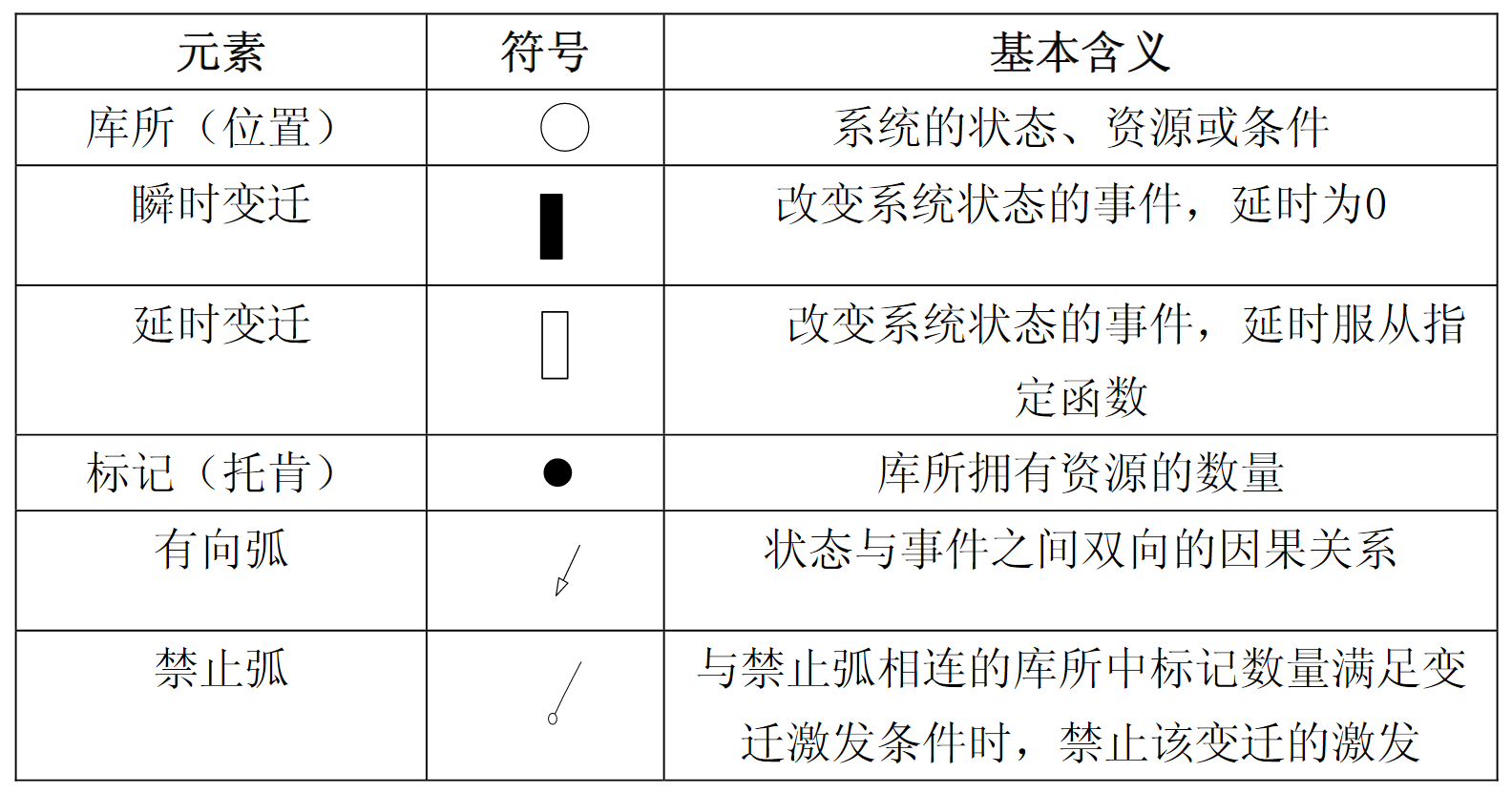
广义随机 Petri 网 (GSPN)
Petri 网的基础知识和建模工具介绍
Petri Net
ISO/IEC 15909 (Systems and software engineering — High-level Petri nets)《系统和软件工程 - 高级 Petri 网》
书籍
- 《Petri网导论》 - 吴哲辉
- 《随机Petri网与系统性能分析》 - 林闯
- 《Petri网原理与应用》 - 袁崇义
Petri 网在系统可靠性分析中的应用主要有以下几个方面:基本行为描述、故障树的表示与简化、可靠性指标的解析计算以及可靠性仿真等
基本 Petri 网
Petri 网( PN ) 为一个三元组,即 $PN=(P,T;F)$ ,其中:
- $P=(p_1,p_2,\cdots p_n)$ 为有限库所集, $n$ 为库所个数;
- $T=(t_1,t_2,\cdots t_m)$ 为有限变迁集, $m$ 为变迁个数;
- $P\cap T=\emptyset $ ,即库所集合 $P$ 和变迁集合 $T$ 不相交;$P\cup T\neq\emptyset$ ,即库所集合 $P$ 和变迁集合 $T$ 不同时为空;
- $F\subseteq(P{\times}T)\cup(T{\times}P)$ 为流关系,即弧集合;
- $dom(F)\bigcup cod(F)=P\bigcup T$ ,即没有孤立元素,其中 $dom(F)={x\mid\exists y:(x,y)\in F}$,$cod(F)={y\mid\exists x:(x,y)\in F}$ 分别为 $F$ 的定义域和值域;
- 集合 $X=P\cup T$ 是网元素集合。
库所/变迁(P/T)系统为一个六元组 $\Sigma=\left(P,T;F,K,W,M_0\right)$ ,其中:
- $PN=(P,T;F)$ 是一个网, $P$ 元素是位置,$T$ 元素是变迁;
- $K:\ P\to N^+\cup{\infty}$ 称为位置容量函数(capacity function),容量表示每个位置存储资源的最大数量,但它不是当前实际的资源数量;
- $W:F\to N^+$ 称为 $PN$ 上的弧权函数,表示实际消耗或产生的资源量;
- $M_0:P\to N$ 是 $PN$ 初始的标识(marking),满足:$\forall p\in P:M_0(p)\leq K(p)$ ,标识是标记在库所中的一种分布。
Petri 网的图形化表述为一种网状模型:
- 库所(Place)
- 变迁(Transition)
- 有向弧(Connection)
- 令牌(token)
Petri 网的主要性质:
- 结构性质:和Petri网初始标识无关的性质
- 动态性质:可达性、活性与死锁、冲突、可逆性、可覆盖性、有界性、安全性
随机 Petri 网
Stochastic Petri Nets(SPN)
把固定时间参数引入Petri网的网模型叫做时间Petri网,在每个变迁的可激发与激发之间联系一个随机的延迟时间,这种类型的Petri网叫做随机Petri网(SPN)。
随机Petri网 $SPN=(P,T;F,W,M_0,\lambda)$ ,其中 $(P,T;F,W,M_0)$ 是一 个 $P/T$ 系统, $\lambda={\lambda_1,\lambda_2,\cdots,\lambda_m}$ 是变迁平均实施速率集合。
$\lambda_i$ 是变迁 $t_{i}\in T$ 的平均实施速率,表示在可实施的情况下单位时间内平均实 施次数,单位是 次数/单位时间。在机械可靠性研究中,$\lambda_i$ 可用来表示零部件的故障率及维修率。
大多数随机Petri网的性能分析是建立在其状态空间与马尔可夫链同构的基础上的。随机Petri网为系统的性能模型提供良好的描述手段;随机马尔可夫过程为模型的评价提供坚实的数学基础。
广义随机 Petri 网
Generalized Stochastic Petri nets (GSPN)
SPN的状态空间会随着问题的增大而指数性地增长,使得SPN同构的MC难以求解。广义随机Petri网(generalized stochastic Petri nets,GSPN)的提出为缓解状态爆炸提供了一种途径。
GSPN是SPN的一种扩充,主要表现在将变迁分成两类:
- 一种为瞬时变迁与随机开关关联(根据一个概率分布函数)且实施延时为零;
- 令一种为时间变迁与指数随机分布的实施延时相关联。
一个 $GSPN=(P,T;F,W,M_0,\lambda)$ ,其中:
- $P$,$W$,$M_0$,$\lambda$ 与 $SPN$ 的定义相同;
- $F$ 中允许有禁止弧,禁止弧仅存在于从库所到变迁的弧。禁止弧所连接的库所的原可实施条件变为不可实施(disenable)条件,原不可实施条件变为可实施条件,且在相连变迁实施时,没有标记从相连的库所移出;
- 变迁集 $T$ 划分为两个子集:$T=T_t\cup T_i$ ,$T_t\cap T_i=\emptyset $ ,时间(timed)变迁集 $T_t=\left{t_1,t_2,\cdots,t_k\right}$ ,瞬时(immediate)变迁集 $T_{i}=\left{t_{k+1},t_{k+2},\cdots,t_{n}\right}$ ,与时间变迁集相关联的平均实施速率集合 $\lambda={\lambda_1,\lambda_2,\cdots,\lambda_t}$。
- 为在一个标识 $M$ 下多个可实施瞬时变迁定义一个随机开关,确定他们之间实施概率选择。
$GSPN$ 建模元素的图形化表示:
分析方法
Petri 网分析方法:
- 可达树(可达图)
- 关联矩阵
- 状态方程
- 化简分析
- 马尔科夫链同构
- 仿真模拟
马尔科夫链同构法:
马尔科夫 $GSPN$ 模型,能通过数值分析或者仿真分析的方法,可以得到库所中标记转移概率、变迁的激发概率的瞬态变化过程以及稳态结果;非马尔科夫 $GSPN$ 网络,只能通过仿真的方式来分析,主要得到库所标记转移和变迁激发的稳态结果。
当Petri网变迁的时延服从指数分布时,一个Petri网同构于一个连续时间马尔可夫链(MC),每个标识对应马尔可夫链的一个状态。两者同构的条件有两个,一个是变迁的实施速率服从指数分布所导致的无记忆性,另一个是标识的可数性。在Petri网模型的可达图上可以很容易地获得 MC 转移速率矩阵的参数,能够计算出 MC的每个状态(标识)的稳定状态下的稳定概率,对Petri网进行分析。
- PN Generation
- Deadlock and Liveness Analysis
- Model Parameter Assignment
- Performance Analysis
- Reachability Graph Creation
- Markov Chain Creation
- Transition Probability Computation
- Design Matrix Evaluation
- Reliability Prediction
- Sensitivity analysis
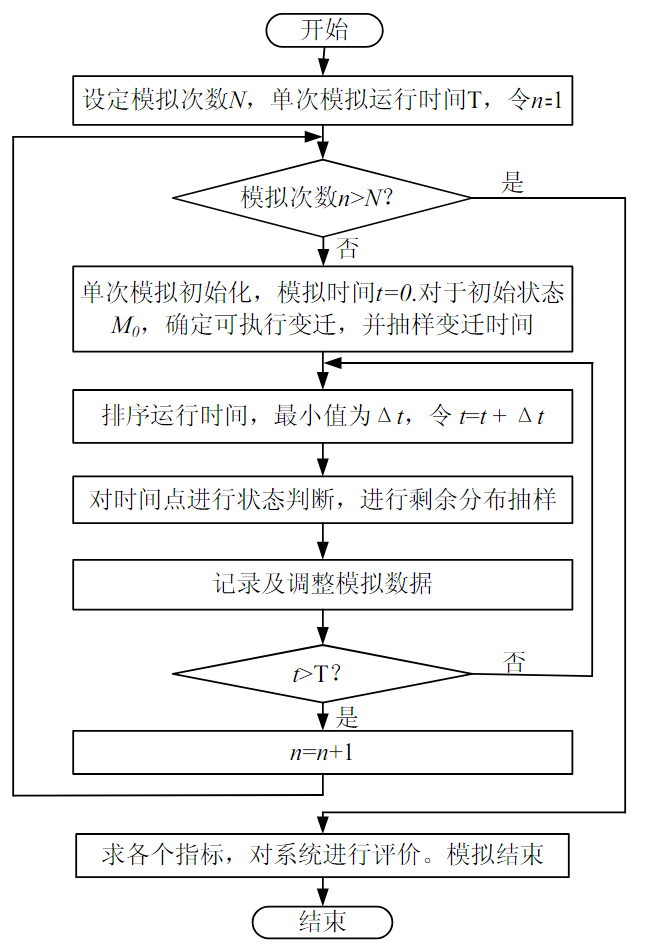
蒙特卡罗模拟法:
通过逆变换从指数分布采样,$t=\frac{-\ln(K)}{\lambda}$,$K$ 的取值范围是 $[0,1]$ ,利用蒙特卡洛模拟可以确定 $K$ 的取值进而每一步仿真得到随机延迟 $t$,进而进行petri 网模型的模拟。
基于 Petri 网的蒙特卡洛模拟流程:
CTMC 求解
GSPN 模型可达集同构于连续时间马尔可夫链 (Continuous-time Markov chain,CTMC)
求解步骤:
- 构建转移速率矩阵
- Kolmogorov 正向方程 $\boldsymbol{P}^{\prime}(t)=\boldsymbol{P}(t)\boldsymbol{Q}$
- 实存状态的稳态概率满足:$\begin{cases}P\cdot Q=0\\sum_{i=1}^lP_i=1&\end{cases}$
- 三个式子组成方程组,求解即为稳态:
- $P=[p_1,p_2,\ldots,p_n]$,是稳态概率分布的向量,其中 $p_{i}$ 表示状态 $i$ 的稳态概率
- Kolmogorov 正向方程:$\frac d{dt}P(t)=P(t)\cdot Q$
- 平衡方程:$P\cdot Q=0$
- P 的和为1:$\sum_{i=1}^np_i=1$
案例分析:
稳态概率向量:$P=[p_0,p_2,\ldots,p_8]$
转移速率矩阵:
$Q = \begin{bmatrix}
& M_0 & M_1 & M_2 & M_3 & M_4 & M_5 & M_6 & M_7 & M_8 \
M_0 & q_{00} & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \
M_1 & \lambda_{15} & q_{11} & \lambda_{6} & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 & 0 & 0 \
M_2 & \lambda_{15} & 0 & q_{22} & 0 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 & 0 \
M_3 & 0 & \lambda_{15} & 0 & q_{33} & \lambda_6 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 \
M_4 & 0 & 0 & \lambda_{15} & 0 & q_{44} & 0 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 \
M_5 & 0 & 0 & 0 & \lambda_{15} & 0 & q_{55} & \lambda_{6} & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 \
M_6 & 0 & 0 & 0 & 0 & \lambda_{15} & 0 & q_{66} & 0 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} \
M_7 & 0 & 0 & 0 & 0 & 0 & \lambda_{15} & 0 & q_{77} & \lambda_{6} \
M_8 & 0 & 0 & 0 & 0 & 0 & 0 & \lambda_{15} & 0 & q_{88}
\end{bmatrix}$
$q_{ii}=-\sum_{j\neq i}q_{ij}$
$\lambda_a = \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}$
$Q = \begin{bmatrix}
& M_0 & M_1 & M_2 & M_3 & M_4 & M_5 & M_6 & M_7 & M_8 \
M_0 & -(\lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}) & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \
M_1 & \lambda_{15} & -(\lambda_{15} + \lambda_{6} + \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}) & \lambda_{6} & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 & 0 & 0 \
M_2 & \lambda_{15} & 0 & -(\lambda_{15} + \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}) & 0 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 & 0 \
M_3 & 0 & \lambda_{15} & 0 & -(\lambda_{15} + \lambda_6 + \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}) & \lambda_6 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 & 0 \
M_4 & 0 & 0 & \lambda_{15} & 0 & -(\lambda_{15} + \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}) & 0 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 & 0 \
M_5 & 0 & 0 & 0 & \lambda_{15} & 0 & -(\lambda_{15} + \lambda_{6} + \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}) & \lambda_{6} & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} & 0 \
M_6 & 0 & 0 & 0 & 0 & \lambda_{15} & 0 & -(\lambda_{15} + \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13}) & 0 & \lambda_7+\lambda_9+\lambda_{11}+\lambda_{13} \
M_7 & 0 & 0 & 0 & 0 & 0 & \lambda_{15} & 0 & -(\lambda_{15} + \lambda_{6}) & \lambda_{6} \
M_8 & 0 & 0 & 0 & 0 & 0 & 0 & \lambda_{15} & 0 & -\lambda_{15}
\end{bmatrix}$
解方程组:
$P(0)=[1,0,0,0,0,0,0,0,0]$,$M_0$为初态
$\frac d{dt}P(t)=P(t)\cdot Q$
$\begin{cases}{P}^{\prime}(t)={P}(0)\cdot Q\P(t=\infty)\cdot Q=0\\sum_{i=0}^8P_i=1&\end{cases}$
这个方程组描述了连续时间马尔可夫链的稳态概率。在这里,$P(t)$ 是状态分布向量,$Q$ 是状态转移速率矩阵。
首先,我们可以通过解微分方程 $\frac d{dt}P(t)=P(0)\cdot Q$ 来得到稳态概率分布,这个微分方程的解是 $P(t)=P(0)\cdot e^{tQ}$
接下来,我们需要找到稳态概率分布 $P(t=\infty)$,这可以通过解方程 $P(t=\infty)\cdot Q=0$ 来实现。解这个方程可以得到马尔可夫链的稳态概率分布。
最后,我们需要确保概率分布的总和为1,即$\sum_{i=0}^8P_i=1$
使用 python 求解:
1 | import numpy as np |
1 | import numpy as np |
使用 Mathematica 求解:
1 | (*定义未知向量 P*)P = Array[p, 9]; |
性能分析
- 稳态概率:分析系统达到稳态时不同库所令牌分布的概率。这有助于了解系统在长期运行中各个状态的概率分布。
- 吞吐量:计算系统在单位时间内完成的任务数或处理的事务数量。吞吐量是衡量系统性能的一个重要指标。
- 平均延迟:计算任务或事务从提交到完成所需的平均时间。平均延迟是衡量系统响应时间的指标。
- 资源利用率:分析系统中各个资源(如处理器、内存等)的利用率,以评估资源的使用效率。
- 并发性:分析系统中并发执行的任务或事务数量,了解系统的并行处理能力。
- 死锁分析:检查系统是否存在死锁情况,即无法进行任何进一步状态转移的情况。
- 故障分析:通过引入故障或随机性来模拟系统的可靠性,以评估系统在故障情况下的性能表现。
- 灵敏度分析:分析系统参数的变化对性能指标的影响,帮助优化系统设计和参数配置。
- 优化:根据性能分析的结果,优化系统结构、资源分配或策略,以提高系统性能。
建模工具
- PIPE
PIPE 5 is currently in beta stage due to an entire re-write of the back end and so is missing most of the analysis modules. If you require Petri net analysis, please use PIPE 4. - CPN IDE
CPN Tools has been replaced now by CPN IDE. Development on CPN Tools has stopped. - TimeNET
- Net Toolbox for MATLAB
- GRIF Petri – Petri Net software(收费)
PIPE
TimeNET
Objects
Places
Exponential transitions
指数跃迁的激发速率必须通过取其倒数来转换为延迟
Immediate transitions
Arc
Inhibitor arcs
Constant definition
Performance measures
Validate
- Statespace 状态空间
Traps 陷阱
- Siphons 虹吸管
Analysis
Transient
运行一周后,系统仍然可运行的概率是多少?
制造系统重新设置后一小时生产了多少零件?
Stationary (Steady-State)
通信通道的最大带宽是多少?
制造系统缓冲区中的预期零件数量是多少?
Analysis
通过对可达性图的充分探索来进行直接、准确的数值性能评估
Approximation
也是直接数值技术,但尝试通过允许某种不准确性来避免一些昂贵的评估部分
Simulation
不计算可达性图,而是遵循标准蒙特卡罗风格模拟方法并进行一些改进
Evaluation
概率与统计
概率分布(Poisson Distribution)就是在统计图中表示概率,横轴是数据的值,纵轴是横轴上对应数据值的概率。
泊松分布
某个时间范围内,发生某件事情x次的概率是多大,如一个月内某机器损坏的次数。若某事件的发生是完全随机的,则在单位时间(或空间)事件发生0次、1次、2次、…、X次相应的概率为:
$$
P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!},k=0,1,2,\cdots
$$
则称该事件的发生服从参数为 $𝜆$ 的Poisson分布,$𝜆$ 是其唯一参数,为Poisson分布的均数(𝜆>0),式中 $e =2.71828$ 为自然对数的底,是常数,$X$ 是事件发生次数,$P(X)$ 为事件发生次数为 $X$ 时的概率。
指数分布
指数分布(Exponential distribution)是一种形式简单地连续型分布,传统上常用于表述电子元器件或某些产品的寿命分布规律。若产品在一定时间区间内的失效数服从泊松分布,则该产品的寿命服从指数分布。若产品的寿命分布服从指数分布,则其失效率为常数。
指数分布的故障密度函数(概率密度函数)为:
$$
f(x)=\left{\begin{array}{cc}{\lambda}e^{-{\lambda}x}&,&x\geq0,\0&,&x<0.\end{array}\right.
$$
累积分布函数为:
$$
F(x)=\left{\begin{array}{cc}1-e^{-{\lambda}x}&,&x\geq0,\0&,&x<0.\end{array}\right.
$$
指数分布具有“无记忆性”,这是指数分布的重要性质。即产品的寿命服从指数分布,则已工作了 t 时间正常的产品,在 t 时间以后的剩余寿命与新的产品一样,与 t 无关。
威布尔分布
威布尔分布(Weibull distribution)在可靠性工程中被广泛使用。威布尔分布有三参数和两参数两种形式。
三参数威布尔分布的概率密度函数为:
$$
f(t)=\begin{cases}\dfrac{m}{t}(t-\gamma)^{m-1}\exp[-\dfrac{(t-\gamma)^m}{t_0}]&&t\geq\gamma\l_0&&t<\gamma&\end{cases}
$$
三参数威布尔分布记为 $T\sim W(m,t_0,\gamma)$,其中 m 为形状参数, $t_0$为尺度参数,$\gamma$ 为位置参数,其取值范围都是$(0,\infty)$ 。
在可靠性工程中,通常取 $\gamma$ = 0,则三参数威布尔分布简化为两参数威布尔分布,其概率密度函数为:
$$
f(t)=\frac{m}{t_0}t^{m-1}\exp(-\frac{t^m}{t_0})\quad\quad t\geq0
$$
根据 m 值的不同,威布尔分布等价或近似于其他分布。例如,当 m = 1 时, 威布尔分布等同于指数分布;当 m =2.5 时,威布尔分布近似于对数正态分布; 当 m = 3.6 时,威布尔分布近似于正态分布。
由于威布尔分布的参数众多,指数分布、正态分布、瑞利分布等均可看作是它特例,所以它适用范围很广。 国外常把它作为机械产品和电子产品的通用故障分布,每当遇到故障分布很不明显,难以断定时,就当威布尔分布来统计、检验, 在工程上往往可得到圆满的结果。
逆变换采样
在已知任意概率分布的累积分布函数时,可用于从该分布中生成随机样本。即,生成符合特定概率分布的随机数。
从指数分布采样:
指数分布的概率密度
$$
f(x;\lambda)=\left{\begin{array}{ll}\lambda e^{-\lambda x}&,&\quad x\geq0,\0&,&\quad x<0.\end{array}\right.
$$
从采样逆变换可知,如果我们让指数分布的累积分布函数服从均匀分布,那么其逆函数服从指数分布,
$$
P(x)=\mathrm{P}(V\leqslant x)=\int_0^xp(x)\mathrm{d}x=1-\mathrm{e}^{-{\lambda}x}
$$
求逆函数:
$$
x=\frac{-\ln(1-u)}{\lambda}
$$
因此从均匀分布 $U[0,1]$ 中采样一系列的 $u_i$ ,代入上式得到的 $xi$ 就是符合指数分布的随机变量。
$xi$ (随机延迟时间)服从指数分布,用于模拟随机Petri网中时间变迁的触发间隔
置信区间
置信水平(Confidence Intervals):区间包含总体平均值的概率
置信区间(Confidence Level):误差范围
95%置信区间表示在重复抽样的情况下,有95%的概率包含了总体参数的真实值。置信区间通常以估计值加减一个误差范围来表示。当我们进行蒙特卡罗模拟时,会生成大量的随机样本,并基于这些样本进行统计分析。利用蒙特卡罗模拟得到的参数估计值和方差(或标准差),我们可以计算置信区间。
蒙特卡罗模拟
蒙特卡罗方法(Monte Carlo method),也称统计模拟方法,是1940年代中期由于科学技术的发展和电子计算机的发明,而提出的一种以概率统计理论为指导的数值计算方法。作为一种常用的模拟技术,其主要出现在风险管理知识领域中的定量风险分析过程,是用于做项目定量风险分析的工具之一,同时蒙特卡洛模拟也可以用于估算进度或成本以及制定进度计划等。
蒙特卡罗仿真的基本流程如下:
- 系统建模。根据系统的目标和结构构建一个合理的数学逻辑模型。建模型的方法有多种,如对系统的动态变化建立系统的 SPN 模型。
- 确定随机变量及其分布,在可靠性仿真中,元件的寿命分布和维修时间分布是仿真的基础,这些分布函数的获得可以通过以往的经验及大量统计来完成。
- 确定随机变量的分布后,选择适当的随机变量抽样方法,实现对已知概率分布抽样。即通过产生随机数的方式进行对已知概率分布的抽样。这是蒙特卡罗仿真最为主要的一步,也是蒙特卡罗仿真思想的体现。
- 统计计算。得到仿真数据后,对系统及元件进行可靠性指标分析。